How High is that Similar Triangle?
Overview & Major Themes
During battle, some of Constitution’s Marines and sailors were stationed 85 to 90 feet above the deck. With this lesson, teach your students to use similar triangles and congruent angles with “shadow reckoning” to find out the height of a tall object on your school grounds. Students then have the opportunity to see how high 85 to 90 feet is off the ground, by comparing it to something similar in height.
Objectives
- Students use shadow reckoning, measurements, and algebra to determine the height of an object on the school grounds and then apply the formula to answer questions.
Outcomes
- Students will learn that similar triangles have sides that are proportional.
- Students will apply this knowledge to solve further equations and find the height of the Maintop, where some of Constitution’s sailors fought during the War of 1812.
Materials & Resources
- Graph Paper
- Copies of attached worksheet
- A sunny day
- Flagpole or any tall, narrow object on the school’s grounds
- Tape measure and a Meter or Yard Stick
- Calculators (optional)
- Illustrations of the “Maintop in Battle” and/or “Sailor’s Aloft”
Instructional Activity
5 min.
With students, view the illustrations of “Maintop in Battle” and/or “Sailor’s Aloft.” Explain to them that on Constitution, some Marines and sailors were high above the deck during battle. Can they imagine how high that is? Explain to them that today, they will find a similar height by finding the height of a tall object on the school grounds.
5 min.
Write the word “similar” and discuss its everyday meaning (looks the same but different; having certain things in common). Ask the students, how are similar figures used in real life today? (Examples: mostly in design for larger structures/objects – scale models, blueprints; also in photo or copy enlargements.)
2 min.
Discuss how the word similar is used in math. Geometric shapes can have the same shape but are not necessarily the same size. Draw an example of two squares, one larger than the other. Explore triangles that are similar in shape but not in size. Have students draw a triangle on the graph paper.
2 min.
Ask the students to then construct a similar triangle, but by doubling the size (have them count the number of squares on the graph paper and double the lengths of the sides).
10 min.
Compare and contrast the first and second triangle: make a chart together on the board of everyone’s first and second triangles. How many blocks are they high, how many blocks are they wide? Are the angles similar? Students should find that corresponding angles are congruent in the similar triangles.
5 min.
Now, integrate math. Show students how the corresponding sides of the triangle are proportional using fractions and cross-multiplication. For example, if a triangle is 5 boxes wide, and 4 boxes high, and its similar triangle is 8 boxes wide with an unknown height:
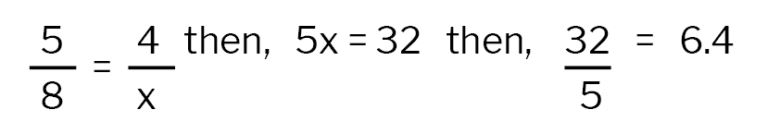
2 min.
Explain to the class that they will be using similar triangles to determine the height of the school’s flagpole (or other object that you have chosen on the school’s grounds), and then they will compare the flagpole to Constitution’s Maintop where Marines were stationed during battle.
2 min.
The method they will use is not only through similar triangles, but also a technique called “shadow reckoning”. Thales, a Greek mathematician first used it in ancient Egypt to determine the height of the pyramids.
5 min.
Hand out the worksheet attached to the Lesson Plan, and work through the steps of shadow reckoning on the first page in the classroom.
5 min.
The height of the flagpole and the stick are a vertical measurement, so they have two right angles (90 degrees).
The sun is a fixed point in the sky (and is far away), and it is assumed its rays are parallel, therefore the sun’s rays create a congruent angle at the top of the pole and the top of the stick. Finally, because the two right triangles are similar, we can write a proportion and find the needed height, x.
20 min.
Once students have worked through the method in the classroom, take them outside to measure the flagpole’s shadow and the shadow of the stick. Then measure the height of the meter or yard stick.
10 min.
Conclusion: Marines on the maintop stood 85 to 90 feet above the decks of the ship. Have students convert their metric measurements to feet and answer these questions: How does the height of the flagpole on the school grounds compare to that height? The full height of the mainmast is 220 feet, how do the three heights compare (maintop, mainmast, flagpole)?

